

Therefore, the straight path that connects these entries (or elements) diagonally is called the leading diagonal of the rectangular matrix $B$. The arrangement of the elements can be expressed in a matrix form as follows. Leading diagonal of a rectangular matrixįor example, we have some entries and they are arranged in $m$ rows and $n$ columns.Primary diagonal of a rectangular matrix.Principal diagonal of a rectangular matrix.An important example of this is the Fourier transform, which diagonalizes constant coefficient differentiation operators (or more generally translation invariant operators), such as the Laplacian operator, say, in the heat equation.Įspecially easy are multiplication operators, which are defined as multiplication by (the values of) a fixed function–the values of the function at each point correspond to the diagonal entries of a matrix.The main diagonal of a rectangular matrix is also called by the following four names alternatively in mathematics. Therefore, a key technique to understanding operators is a change of coordinates-in the language of operators, an integral transform-which changes the basis to an eigenbasis of eigenfunctions: which makes the equation separable. In operator theory, particularly the study of PDEs, operators are particularly easy to understand and PDEs easy to solve if the operator is diagonal with respect to the basis with which one is working this corresponds to a separable partial differential equation. Furthermore, the singular value decomposition implies that for any matrix A, there exist unitary matrices U and V such that U ∗AV is diagonal with positive entries. The spectral theorem says that every normal matrix is unitarily similar to a diagonal matrix (if AA ∗ = A ∗ A then there exists a unitary matrix U such that UAU ∗ is diagonal). A simple consequence of this is that if UAU D (where D diagonal and U unitary), then AU UD and hence A has n orthonormal eigenvectors. Your ready to hang artwork is printed on canvas then stretched and. Over the field of real or complex numbers, more is true. Recall the denition of a unitarily diagonalizable matrix: A matrix A Mn is called unitarily diagonalizable if there is a unitary matrix U for which UAU is diagonal. Shop Giant Art 20 x 16 Diagonal Matrix I Art Block Framed Canvas online at. Such matrices are said to be diagonalizable. In fact, a given n-by- n matrix A is similar to a diagonal matrix (meaning that there is a matrix X such that X −1 AX is diagonal) if and only if it has n linearly independent eigenvectors.
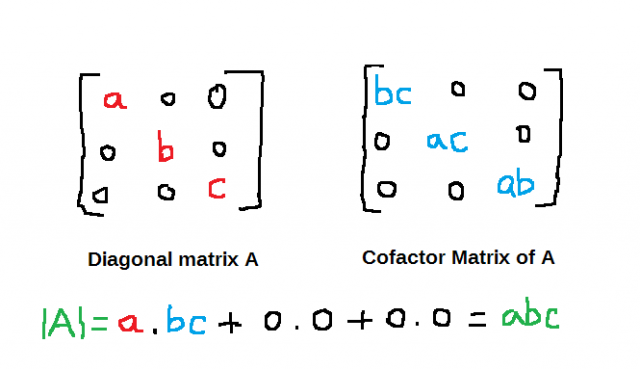
Because of the simple description of the matrix operation and eigenvalues/eigenvectors given above, it is typically desirable to represent a given matrix or linear map by a diagonal matrix. The identity matrix I n and zero matrix are diagonal.ĭiagonal matrices occur in many areas of linear algebra.A matrix is diagonal if and only if it is both upper- and lower-triangular.A matrix is diagonal if and only if it is triangular and normal.The adjugate of a diagonal matrix is again diagonal., λ n with associated eigenvectors of e 1. In other words, the eigenvalues of diag( λ 1. The resulting equation is known as eigenvalue equation and used to derive the characteristic polynomial and, further, eigenvalues and eigenvectors. Elements of the main diagonal can either be zero or nonzero. As a linear transformation, an orthogonal matrix. The determinant of any orthogonal matrix is either +1 or 1. In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero the term usually refers to square matrices. An orthogonal matrix Q is necessarily invertible (with inverse Q1 QT ), unitary ( Q1 Q ), where Q is the Hermitian adjoint ( conjugate transpose) of Q, and therefore normal ( QQ QQ) over the real numbers. Matrix whose only nonzero elements are on its main diagonal


 0 kommentar(er)
0 kommentar(er)
